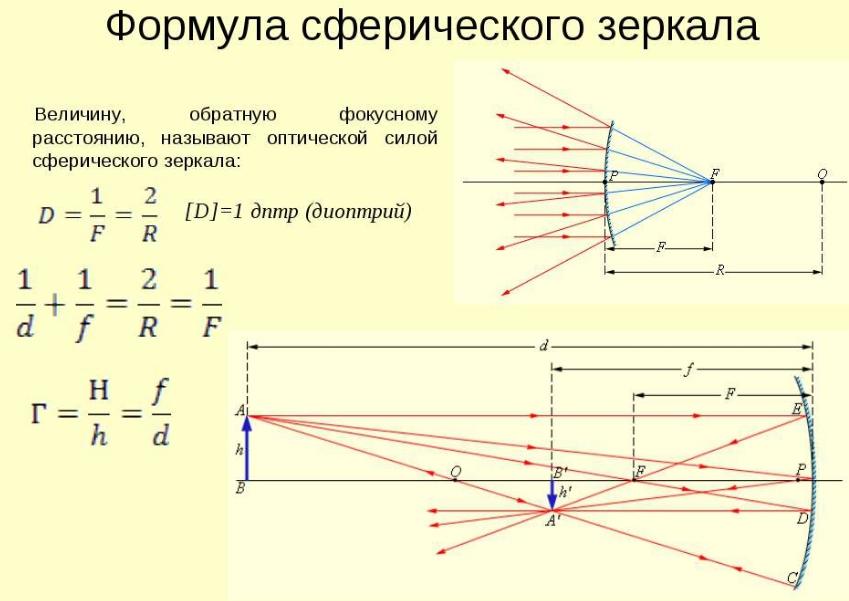
ಬೆಳಕಿನ ಪ್ರತಿಫಲನದ ನಿಯಮಗಳು ಮತ್ತು ಅವರ ಆವಿಷ್ಕಾರದ ಇತಿಹಾಸ
ಬೆಳಕಿನ ಪ್ರತಿಫಲನದ ನಿಯಮವನ್ನು ವೀಕ್ಷಣೆಗಳು ಮತ್ತು ಪ್ರಯೋಗಗಳ ಮೂಲಕ ಕಂಡುಹಿಡಿಯಲಾಯಿತು. ಸಹಜವಾಗಿ, ಇದನ್ನು ಸೈದ್ಧಾಂತಿಕವಾಗಿ ಪಡೆಯಬಹುದು, ಆದರೆ ಈಗ ಬಳಸಲಾಗುವ ಎಲ್ಲಾ ತತ್ವಗಳನ್ನು ಆಚರಣೆಯಲ್ಲಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ ಮತ್ತು ಸಮರ್ಥಿಸಲಾಗಿದೆ. ಈ ವಿದ್ಯಮಾನದ ಮುಖ್ಯ ಲಕ್ಷಣಗಳನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು ಬೆಳಕಿನ ಯೋಜನೆ ಮತ್ತು ಸಲಕರಣೆಗಳ ಆಯ್ಕೆಗೆ ಸಹಾಯ ಮಾಡುತ್ತದೆ. ಈ ತತ್ವವು ಇತರ ಕ್ಷೇತ್ರಗಳಲ್ಲಿಯೂ ಸಹ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ - ರೇಡಿಯೋ ತರಂಗಗಳು, ಕ್ಷ-ಕಿರಣಗಳು, ಇತ್ಯಾದಿ. ಪ್ರತಿಬಿಂಬದಲ್ಲಿ ನಿಖರವಾಗಿ ಅದೇ ರೀತಿ ವರ್ತಿಸಿ.
ಬೆಳಕಿನ ಪ್ರತಿಫಲನ ಮತ್ತು ಅದರ ಪ್ರಭೇದಗಳು, ಯಾಂತ್ರಿಕತೆ ಏನು
ಕಾನೂನನ್ನು ಈ ಕೆಳಗಿನಂತೆ ರೂಪಿಸಲಾಗಿದೆ: ಘಟನೆ ಮತ್ತು ಪ್ರತಿಫಲಿತ ಕಿರಣಗಳು ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಇರುತ್ತವೆ, ಪ್ರತಿಫಲಿಸುವ ಮೇಲ್ಮೈಗೆ ಲಂಬವಾಗಿರುತ್ತವೆ, ಇದು ಘಟನೆಯ ಹಂತದಿಂದ ಹೊರಹೊಮ್ಮುತ್ತದೆ. ಘಟನೆಯ ಕೋನವು ಪ್ರತಿಫಲನದ ಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಮೂಲಭೂತವಾಗಿ, ಪ್ರತಿಫಲನವು ಒಂದು ಭೌತಿಕ ಪ್ರಕ್ರಿಯೆಯಾಗಿದ್ದು, ಇದರಲ್ಲಿ ಕಿರಣ, ಕಣಗಳು ಅಥವಾ ವಿಕಿರಣವು ಸಮತಲದೊಂದಿಗೆ ಸಂವಹನ ನಡೆಸುತ್ತದೆ. ಅಲೆಗಳ ದಿಕ್ಕು ಎರಡು ಮಾಧ್ಯಮಗಳ ಗಡಿಯಲ್ಲಿ ಬದಲಾಗುತ್ತದೆ, ಏಕೆಂದರೆ ಅವುಗಳು ವಿಭಿನ್ನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿವೆ.ಪ್ರತಿಫಲಿತ ಬೆಳಕು ಯಾವಾಗಲೂ ಅದು ಬಂದ ಮಾಧ್ಯಮಕ್ಕೆ ಹಿಂತಿರುಗುತ್ತದೆ. ಹೆಚ್ಚಾಗಿ ಪ್ರತಿಫಲನದ ಸಮಯದಲ್ಲಿ, ಅಲೆಗಳ ವಕ್ರೀಭವನದ ವಿದ್ಯಮಾನವನ್ನು ಸಹ ಗಮನಿಸಬಹುದು.
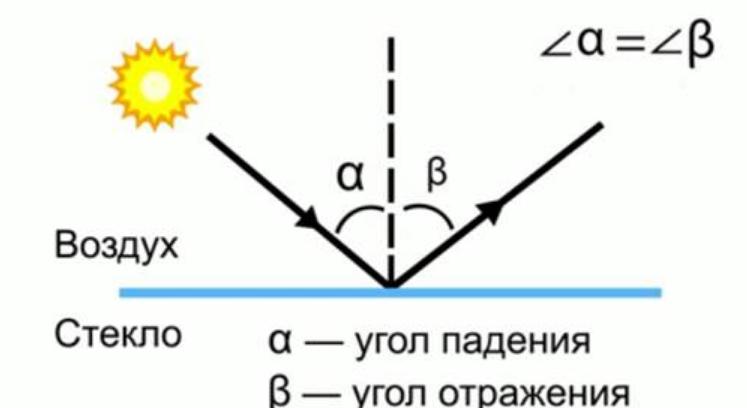
ಕನ್ನಡಿ ಪ್ರತಿಬಿಂಬ
ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಪ್ರತಿಫಲಿತ ಮತ್ತು ಘಟನೆಯ ಕಿರಣಗಳ ನಡುವೆ ಸ್ಪಷ್ಟವಾದ ಸಂಬಂಧವಿದೆ, ಇದು ಈ ವಿಧದ ಮುಖ್ಯ ಲಕ್ಷಣವಾಗಿದೆ. ಪ್ರತಿಬಿಂಬಿಸಲು ನಿರ್ದಿಷ್ಟವಾದ ಹಲವಾರು ಮುಖ್ಯ ಅಂಶಗಳಿವೆ:
- ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣವು ಯಾವಾಗಲೂ ಘಟನೆಯ ಕಿರಣದ ಮೂಲಕ ಹಾದುಹೋಗುವ ಸಮತಲದಲ್ಲಿರುತ್ತದೆ ಮತ್ತು ಪ್ರತಿಬಿಂಬಿಸುವ ಮೇಲ್ಮೈಗೆ ಸಾಮಾನ್ಯವಾಗಿರುತ್ತದೆ, ಇದು ಘಟನೆಯ ಹಂತದಲ್ಲಿ ಪುನರ್ನಿರ್ಮಾಣವಾಗುತ್ತದೆ.
- ಘಟನೆಯ ಕೋನವು ಬೆಳಕಿನ ಕಿರಣದ ಪ್ರತಿಫಲನದ ಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
- ಪ್ರತಿಫಲಿತ ಕಿರಣದ ಗುಣಲಕ್ಷಣಗಳು ಕಿರಣದ ಕಿರಣದ ಧ್ರುವೀಕರಣ ಮತ್ತು ಅದರ ಘಟನೆಯ ಕೋನಕ್ಕೆ ಅನುಗುಣವಾಗಿರುತ್ತವೆ. ಅಲ್ಲದೆ, ಸೂಚಕವು ಎರಡು ಪರಿಸರಗಳ ಗುಣಲಕ್ಷಣಗಳಿಂದ ಪ್ರಭಾವಿತವಾಗಿರುತ್ತದೆ.
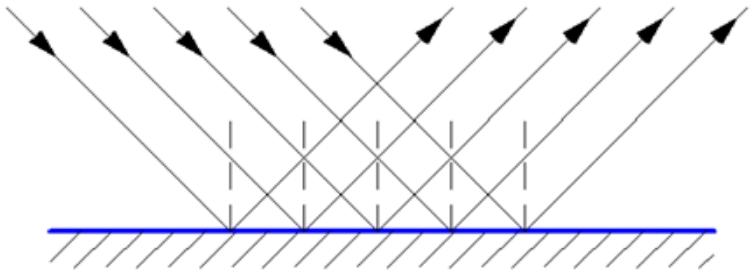
ಈ ಸಂದರ್ಭದಲ್ಲಿ, ವಕ್ರೀಕಾರಕ ಸೂಚ್ಯಂಕಗಳು ಸಮತಲದ ಗುಣಲಕ್ಷಣಗಳು ಮತ್ತು ಬೆಳಕಿನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ನಯವಾದ ಮೇಲ್ಮೈಗಳಿರುವಲ್ಲೆಲ್ಲಾ ಈ ಪ್ರತಿಬಿಂಬವನ್ನು ಕಾಣಬಹುದು. ಆದರೆ ವಿಭಿನ್ನ ಪರಿಸರಗಳಿಗೆ, ಪರಿಸ್ಥಿತಿಗಳು ಮತ್ತು ತತ್ವಗಳು ಬದಲಾಗಬಹುದು.
ಒಟ್ಟು ಆಂತರಿಕ ಪ್ರತಿಬಿಂಬ
ಧ್ವನಿ ಮತ್ತು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳಿಗೆ ವಿಶಿಷ್ಟವಾಗಿದೆ. ಎರಡು ಪರಿಸರಗಳು ಸಂಧಿಸುವ ಹಂತದಲ್ಲಿ ಸಂಭವಿಸುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಪ್ರಸರಣ ವೇಗ ಕಡಿಮೆ ಇರುವ ಮಾಧ್ಯಮದಿಂದ ಅಲೆಗಳು ಬೀಳಬೇಕು. ಬೆಳಕಿಗೆ ಸಂಬಂಧಿಸಿದಂತೆ, ಈ ಸಂದರ್ಭದಲ್ಲಿ ವಕ್ರೀಕಾರಕ ಸೂಚ್ಯಂಕಗಳು ಹೆಚ್ಚು ಹೆಚ್ಚಾಗುತ್ತವೆ ಎಂದು ನಾವು ಹೇಳಬಹುದು.
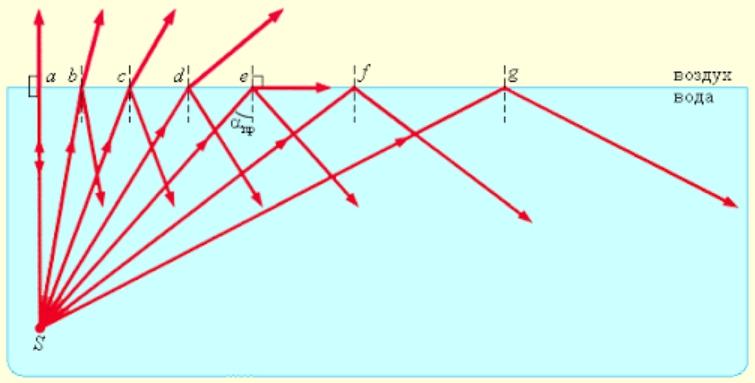
ಬೆಳಕಿನ ಕಿರಣದ ಘಟನೆಯ ಕೋನವು ವಕ್ರೀಭವನದ ಕೋನದ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ. ಅದರ ಮೌಲ್ಯದ ಹೆಚ್ಚಳದೊಂದಿಗೆ, ಪ್ರತಿಫಲಿತ ಕಿರಣಗಳ ತೀವ್ರತೆಯು ಹೆಚ್ಚಾಗುತ್ತದೆ ಮತ್ತು ವಕ್ರೀಭವನವು ಕಡಿಮೆಯಾಗುತ್ತದೆ.ಒಂದು ನಿರ್ದಿಷ್ಟ ನಿರ್ಣಾಯಕ ಮೌಲ್ಯವನ್ನು ತಲುಪಿದಾಗ, ವಕ್ರೀಕಾರಕ ಸೂಚ್ಯಂಕಗಳು ಶೂನ್ಯಕ್ಕೆ ಕಡಿಮೆಯಾಗುತ್ತವೆ, ಇದು ಕಿರಣಗಳ ಒಟ್ಟು ಪ್ರತಿಫಲನಕ್ಕೆ ಕಾರಣವಾಗುತ್ತದೆ.
ನಿರ್ಣಾಯಕ ಕೋನವನ್ನು ವಿವಿಧ ಮಾಧ್ಯಮಗಳಿಗೆ ಪ್ರತ್ಯೇಕವಾಗಿ ಲೆಕ್ಕಹಾಕಲಾಗುತ್ತದೆ.
ಬೆಳಕಿನ ಪ್ರಸರಣ ಪ್ರತಿಫಲನ
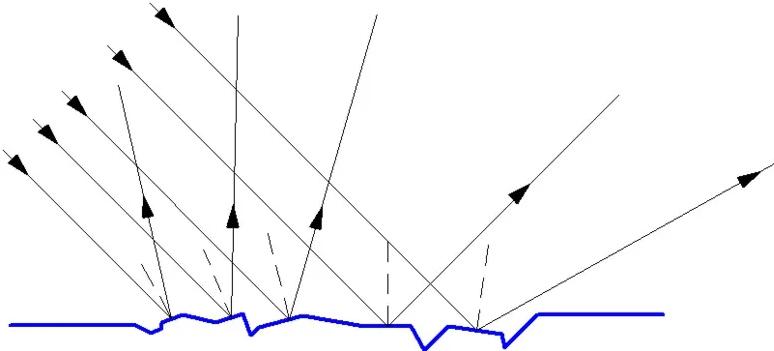
ಈ ಆಯ್ಕೆಯು ಅಸಮ ಮೇಲ್ಮೈಯನ್ನು ಹೊಡೆದಾಗ, ಕಿರಣಗಳು ವಿಭಿನ್ನ ದಿಕ್ಕುಗಳಲ್ಲಿ ಪ್ರತಿಫಲಿಸುತ್ತದೆ ಎಂಬ ಅಂಶದಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟಿದೆ. ಪ್ರತಿಫಲಿತ ಬೆಳಕು ಸರಳವಾಗಿ ಚದುರುತ್ತದೆ ಮತ್ತು ಈ ಕಾರಣದಿಂದಾಗಿ ನಿಮ್ಮ ಪ್ರತಿಬಿಂಬವನ್ನು ಅಸಮ ಅಥವಾ ಮ್ಯಾಟ್ ಮೇಲ್ಮೈಯಲ್ಲಿ ನೀವು ನೋಡಲಾಗುವುದಿಲ್ಲ. ಕಿರಣಗಳ ಪ್ರಸರಣದ ವಿದ್ಯಮಾನವು ಅಸಮಾನತೆಗಳು ತರಂಗಾಂತರಕ್ಕೆ ಸಮಾನವಾದ ಅಥವಾ ಹೆಚ್ಚಿನದಾಗಿದ್ದರೆ ಗಮನಿಸಬಹುದು.
ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಒಂದು ಮತ್ತು ಒಂದೇ ಸಮತಲವು ಬೆಳಕು ಅಥವಾ ನೇರಳಾತೀತಕ್ಕೆ ವ್ಯಾಪಕವಾಗಿ ಪ್ರತಿಫಲಿಸುತ್ತದೆ, ಆದರೆ ಅದೇ ಸಮಯದಲ್ಲಿ ಅತಿಗೆಂಪು ವರ್ಣಪಟಲವನ್ನು ಚೆನ್ನಾಗಿ ಪ್ರತಿಬಿಂಬಿಸುತ್ತದೆ. ಇದು ಎಲ್ಲಾ ಅಲೆಗಳ ಗುಣಲಕ್ಷಣಗಳು ಮತ್ತು ಮೇಲ್ಮೈಯ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.
ಹಿಮ್ಮುಖ ಪ್ರತಿಫಲನ
ಕಿರಣಗಳು, ಅಲೆಗಳು ಅಥವಾ ಇತರ ಕಣಗಳು ಮರಳಿ ಪ್ರತಿಫಲಿಸಿದಾಗ ಈ ವಿದ್ಯಮಾನವನ್ನು ಗಮನಿಸಬಹುದು, ಅಂದರೆ ಮೂಲದ ಕಡೆಗೆ. ಈ ಆಸ್ತಿಯನ್ನು ಖಗೋಳಶಾಸ್ತ್ರ, ನೈಸರ್ಗಿಕ ವಿಜ್ಞಾನ, ಔಷಧ, ಛಾಯಾಗ್ರಹಣ ಮತ್ತು ಇತರ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ಬಳಸಬಹುದು. ದೂರದರ್ಶಕಗಳಲ್ಲಿನ ಪೀನ ಮಸೂರಗಳ ವ್ಯವಸ್ಥೆಯಿಂದಾಗಿ, ಬರಿಗಣ್ಣಿಗೆ ಗೋಚರಿಸದ ನಕ್ಷತ್ರಗಳ ಬೆಳಕನ್ನು ನೋಡಲು ಸಾಧ್ಯವಿದೆ.
ಬೆಳಕು ಮೂಲಕ್ಕೆ ಮರಳಲು ಕೆಲವು ಪರಿಸ್ಥಿತಿಗಳನ್ನು ರಚಿಸುವುದು ಮುಖ್ಯವಾಗಿದೆ, ಇದನ್ನು ಹೆಚ್ಚಾಗಿ ದೃಗ್ವಿಜ್ಞಾನ ಮತ್ತು ಕಿರಣಗಳ ಕಿರಣದ ದಿಕ್ಕಿನ ಮೂಲಕ ಸಾಧಿಸಲಾಗುತ್ತದೆ. ಉದಾಹರಣೆಗೆ, ಈ ತತ್ವವನ್ನು ಅಲ್ಟ್ರಾಸೌಂಡ್ ಅಧ್ಯಯನದಲ್ಲಿ ಬಳಸಲಾಗುತ್ತದೆ, ಪ್ರತಿಫಲಿತ ಅಲ್ಟ್ರಾಸಾನಿಕ್ ತರಂಗಗಳಿಗೆ ಧನ್ಯವಾದಗಳು, ಅಧ್ಯಯನದ ಅಡಿಯಲ್ಲಿ ಅಂಗದ ಚಿತ್ರವನ್ನು ಮಾನಿಟರ್ನಲ್ಲಿ ಪ್ರದರ್ಶಿಸಲಾಗುತ್ತದೆ.
ಪ್ರತಿಬಿಂಬದ ನಿಯಮಗಳ ಆವಿಷ್ಕಾರದ ಇತಿಹಾಸ
ಈ ವಿದ್ಯಮಾನವು ದೀರ್ಘಕಾಲದವರೆಗೆ ತಿಳಿದಿದೆ.ಮೊದಲ ಬಾರಿಗೆ, ಬೆಳಕಿನ ಪ್ರತಿಫಲನವನ್ನು "ಕಟೋಪ್ಟ್ರಿಕ್" ಕೃತಿಯಲ್ಲಿ ಉಲ್ಲೇಖಿಸಲಾಗಿದೆ, ಇದು 200 BC ಯ ಹಿಂದಿನದು. ಮತ್ತು ಪ್ರಾಚೀನ ಗ್ರೀಕ್ ವಿದ್ವಾಂಸ ಯೂಕ್ಲಿಡ್ ಬರೆದಿದ್ದಾರೆ. ಮೊದಲ ಪ್ರಯೋಗಗಳು ಸರಳವಾಗಿದ್ದವು, ಆದ್ದರಿಂದ ಆ ಸಮಯದಲ್ಲಿ ಯಾವುದೇ ಸೈದ್ಧಾಂತಿಕ ಆಧಾರವು ಕಾಣಿಸಿಕೊಂಡಿಲ್ಲ, ಆದರೆ ಅವರು ಈ ವಿದ್ಯಮಾನವನ್ನು ಕಂಡುಹಿಡಿದರು. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಕನ್ನಡಿ ಮೇಲ್ಮೈಗಳಿಗೆ ಫೆರ್ಮಾಟ್ ತತ್ವವನ್ನು ಬಳಸಲಾಯಿತು.
ಫ್ರೆಸ್ನೆಲ್ ಸೂತ್ರಗಳು
ಆಗಸ್ಟೆ ಫ್ರೆಸ್ನೆಲ್ ಅವರು ಫ್ರೆಂಚ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞರಾಗಿದ್ದು, ಅವರು ಇಂದಿಗೂ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುವ ಹಲವಾರು ಸೂತ್ರಗಳನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು. ಪ್ರತಿಫಲಿತ ಮತ್ತು ವಕ್ರೀಭವನದ ವಿದ್ಯುತ್ಕಾಂತೀಯ ಅಲೆಗಳ ತೀವ್ರತೆ ಮತ್ತು ವೈಶಾಲ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಅವುಗಳನ್ನು ಬಳಸಲಾಗುತ್ತದೆ. ಅದೇ ಸಮಯದಲ್ಲಿ, ಅವರು ವಿಭಿನ್ನ ವಕ್ರೀಕಾರಕ ಮೌಲ್ಯಗಳೊಂದಿಗೆ ಎರಡು ಮಾಧ್ಯಮಗಳ ನಡುವಿನ ಸ್ಪಷ್ಟವಾದ ಗಡಿಯನ್ನು ಹಾದುಹೋಗಬೇಕು.
ಫ್ರೆಂಚ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞನ ಸೂತ್ರಗಳಿಗೆ ಸರಿಹೊಂದುವ ಎಲ್ಲಾ ವಿದ್ಯಮಾನಗಳನ್ನು ಫ್ರೆಸ್ನೆಲ್ ಪ್ರತಿಫಲನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಆದರೆ ಮಾಧ್ಯಮವು ಐಸೊಟ್ರೊಪಿಕ್ ಆಗಿದ್ದಾಗ ಮಾತ್ರ ಪಡೆದ ಎಲ್ಲಾ ಕಾನೂನುಗಳು ಮಾನ್ಯವಾಗಿರುತ್ತವೆ ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಗಡಿಯು ಸ್ಪಷ್ಟವಾಗಿದೆ ಎಂದು ನೆನಪಿನಲ್ಲಿಡಬೇಕು. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಘಟನೆಯ ಕೋನವು ಯಾವಾಗಲೂ ಪ್ರತಿಫಲನದ ಕೋನಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ವಕ್ರೀಭವನದ ಮೌಲ್ಯವನ್ನು ಸ್ನೆಲ್ ನಿಯಮದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ.
ಸಮತಟ್ಟಾದ ಮೇಲ್ಮೈಯಲ್ಲಿ ಬೆಳಕು ಬಿದ್ದಾಗ, ಎರಡು ರೀತಿಯ ಧ್ರುವೀಕರಣವು ಇರಬಹುದು:
- p-ಧ್ರುವೀಕರಣವು ವಿದ್ಯುತ್ಕಾಂತೀಯ ಕ್ಷೇತ್ರದ ವೆಕ್ಟರ್ ಘಟನೆಯ ಸಮತಲದಲ್ಲಿದೆ ಎಂಬ ಅಂಶದಿಂದ ನಿರೂಪಿಸಲ್ಪಟ್ಟಿದೆ.
- s-ಧ್ರುವೀಕರಣವು ಮೊದಲ ವಿಧದಿಂದ ಭಿನ್ನವಾಗಿದೆ, ಇದರಲ್ಲಿ ವಿದ್ಯುತ್ಕಾಂತೀಯ ತರಂಗ ತೀವ್ರತೆಯ ವೆಕ್ಟರ್ ಸಮತಲಕ್ಕೆ ಲಂಬವಾಗಿ ಇದೆ, ಇದರಲ್ಲಿ ಘಟನೆ ಮತ್ತು ಪ್ರತಿಫಲಿತ ಕಿರಣ ಎರಡೂ ಇರುತ್ತದೆ.

ವಿಭಿನ್ನ ಧ್ರುವೀಕರಣಗಳೊಂದಿಗೆ ಸನ್ನಿವೇಶಗಳಿಗೆ ಸೂತ್ರಗಳು ಭಿನ್ನವಾಗಿರುತ್ತವೆ.ಧ್ರುವೀಕರಣವು ಕಿರಣದ ಗುಣಲಕ್ಷಣಗಳ ಮೇಲೆ ಪರಿಣಾಮ ಬೀರುತ್ತದೆ ಮತ್ತು ಇದು ವಿಭಿನ್ನ ರೀತಿಯಲ್ಲಿ ಪ್ರತಿಫಲಿಸುತ್ತದೆ ಎಂಬ ಅಂಶದಿಂದಾಗಿ ಇದು ಸಂಭವಿಸುತ್ತದೆ. ಒಂದು ನಿರ್ದಿಷ್ಟ ಕೋನದಲ್ಲಿ ಬೆಳಕು ಬಿದ್ದಾಗ, ಪ್ರತಿಫಲಿತ ಕಿರಣವನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ಧ್ರುವೀಕರಿಸಬಹುದು. ಈ ಕೋನವನ್ನು ಬ್ರೂಸ್ಟರ್ ಕೋನ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಇದು ಇಂಟರ್ಫೇಸ್ನಲ್ಲಿ ಮಾಧ್ಯಮದ ವಕ್ರೀಭವನದ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.
ಅಂದಹಾಗೆ! ಪ್ರತಿಬಿಂಬಿತ ಕಿರಣವು ಯಾವಾಗಲೂ ಧ್ರುವೀಕೃತವಾಗಿರುತ್ತದೆ, ಘಟನೆಯ ಬೆಳಕು ಧ್ರುವೀಕರಿಸದಿದ್ದರೂ ಸಹ.
ಹ್ಯೂಜೆನ್ಸ್ ತತ್ವ
ಹ್ಯೂಜೆನ್ಸ್ ಡಚ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞರಾಗಿದ್ದು, ಅವರು ಯಾವುದೇ ಪ್ರಕೃತಿಯ ಅಲೆಗಳನ್ನು ವಿವರಿಸಲು ಸಾಧ್ಯವಾಗುವಂತೆ ತತ್ವಗಳನ್ನು ಪಡೆಯುವಲ್ಲಿ ಯಶಸ್ವಿಯಾದರು. ಅದರ ಸಹಾಯದಿಂದ ಅವರು ಹೆಚ್ಚಾಗಿ ಪ್ರತಿಬಿಂಬದ ನಿಯಮ ಮತ್ತು ಎರಡನ್ನೂ ಸಾಬೀತುಪಡಿಸುತ್ತಾರೆ ಬೆಳಕಿನ ವಕ್ರೀಭವನದ ನಿಯಮ.
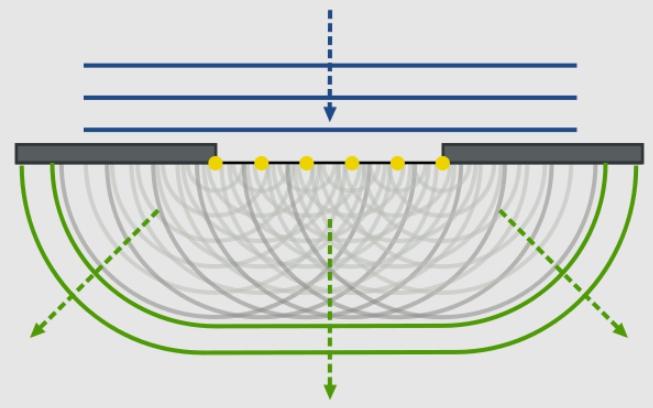
ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಬೆಳಕನ್ನು ಸಮತಟ್ಟಾದ ಆಕಾರದ ತರಂಗ ಎಂದು ಅರ್ಥೈಸಲಾಗುತ್ತದೆ, ಅಂದರೆ, ಎಲ್ಲಾ ತರಂಗ ಮೇಲ್ಮೈಗಳು ಸಮತಟ್ಟಾಗಿರುತ್ತವೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ತರಂಗ ಮೇಲ್ಮೈ ಒಂದೇ ಹಂತದಲ್ಲಿ ಆಂದೋಲನಗಳೊಂದಿಗೆ ಬಿಂದುಗಳ ಗುಂಪಾಗಿದೆ.
ಮಾತುಗಳು ಹೀಗೆ ಸಾಗುತ್ತವೆ: ಪ್ರಕ್ಷುಬ್ಧತೆಯು ತರುವಾಯ ಬಂದ ಯಾವುದೇ ಬಿಂದುವು ಗೋಳಾಕಾರದ ಅಲೆಗಳ ಮೂಲವಾಗುತ್ತದೆ.
ವೀಡಿಯೊದಲ್ಲಿ, ಗ್ರೇಡ್ 8 ಭೌತಶಾಸ್ತ್ರದ ಕಾನೂನನ್ನು ಗ್ರಾಫಿಕ್ಸ್ ಮತ್ತು ಅನಿಮೇಷನ್ ಬಳಸಿ ಸರಳ ಪದಗಳಲ್ಲಿ ವಿವರಿಸಲಾಗಿದೆ.
ಫೆಡೋರೊವ್ ಅವರ ಬದಲಾವಣೆ
ಇದನ್ನು ಫೆಡೋರೊವ್-ಎಂಬರ್ ಪರಿಣಾಮ ಎಂದೂ ಕರೆಯುತ್ತಾರೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಒಟ್ಟು ಆಂತರಿಕ ಪ್ರತಿಫಲನದೊಂದಿಗೆ ಬೆಳಕಿನ ಕಿರಣದ ಸ್ಥಳಾಂತರವಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಶಿಫ್ಟ್ ಅತ್ಯಲ್ಪವಾಗಿದೆ, ಇದು ಯಾವಾಗಲೂ ತರಂಗಾಂತರಕ್ಕಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ. ಈ ಸ್ಥಳಾಂತರದ ಕಾರಣ, ಪ್ರತಿಫಲಿತ ಕಿರಣವು ಘಟನೆಯ ಕಿರಣದಂತೆಯೇ ಅದೇ ಸಮತಲದಲ್ಲಿ ಇರುವುದಿಲ್ಲ, ಇದು ಬೆಳಕಿನ ಪ್ರತಿಫಲನದ ನಿಯಮಕ್ಕೆ ವಿರುದ್ಧವಾಗಿದೆ.
ವೈಜ್ಞಾನಿಕ ಸಂಶೋಧನೆಗಾಗಿ ಡಿಪ್ಲೊಮಾವನ್ನು ಎಫ್.ಐ. 1980 ರಲ್ಲಿ ಫೆಡೋರೊವ್.
ಕಿರಣಗಳ ಪಾರ್ಶ್ವದ ಸ್ಥಳಾಂತರವನ್ನು 1955 ರಲ್ಲಿ ಸೋವಿಯತ್ ವಿಜ್ಞಾನಿಗಳು ಗಣಿತದ ಲೆಕ್ಕಾಚಾರಗಳಿಗೆ ಧನ್ಯವಾದಗಳು ಸೈದ್ಧಾಂತಿಕವಾಗಿ ಸಾಬೀತುಪಡಿಸಿದರು. ಈ ಪರಿಣಾಮದ ಪ್ರಾಯೋಗಿಕ ದೃಢೀಕರಣಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ, ಫ್ರೆಂಚ್ ಭೌತಶಾಸ್ತ್ರಜ್ಞ ಅಂಬರ್ ಸ್ವಲ್ಪ ಸಮಯದ ನಂತರ ಅದನ್ನು ಮಾಡಿದರು.
ಆಚರಣೆಯಲ್ಲಿ ಕಾನೂನಿನ ಬಳಕೆ

ಪ್ರಶ್ನೆಯಲ್ಲಿರುವ ಕಾನೂನು ತೋರುತ್ತಿರುವುದಕ್ಕಿಂತ ಹೆಚ್ಚು ಸಾಮಾನ್ಯವಾಗಿದೆ. ಈ ತತ್ವವನ್ನು ವಿವಿಧ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ:
- ಕನ್ನಡಿ ಸರಳ ಉದಾಹರಣೆಯಾಗಿದೆ. ಇದು ಮೃದುವಾದ ಮೇಲ್ಮೈಯಾಗಿದ್ದು ಅದು ಬೆಳಕು ಮತ್ತು ಇತರ ರೀತಿಯ ವಿಕಿರಣವನ್ನು ಚೆನ್ನಾಗಿ ಪ್ರತಿಬಿಂಬಿಸುತ್ತದೆ. ಫ್ಲಾಟ್ ಆವೃತ್ತಿಗಳು ಮತ್ತು ಇತರ ಆಕಾರಗಳ ಅಂಶಗಳು ಎರಡನ್ನೂ ಬಳಸಲಾಗುತ್ತದೆ, ಉದಾಹರಣೆಗೆ, ಗೋಳಾಕಾರದ ಮೇಲ್ಮೈಗಳು ವಸ್ತುಗಳನ್ನು ದೂರ ಸರಿಸಲು ಅನುವು ಮಾಡಿಕೊಡುತ್ತದೆ, ಇದು ಕಾರಿನಲ್ಲಿ ಹಿಂಬದಿಯ ಕನ್ನಡಿಗಳಂತೆ ಅವುಗಳನ್ನು ಅನಿವಾರ್ಯವಾಗಿಸುತ್ತದೆ.
- ವಿವಿಧ ಆಪ್ಟಿಕಲ್ ಉಪಕರಣಗಳು ಪರಿಗಣಿಸಲಾದ ತತ್ವಗಳ ಕಾರಣದಿಂದಾಗಿ ಸಹ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ. ಇದು ಎಲ್ಲೆಡೆ ಕಂಡುಬರುವ ಕನ್ನಡಕದಿಂದ ಹಿಡಿದು, ಪೀನ ಮಸೂರಗಳನ್ನು ಹೊಂದಿರುವ ಶಕ್ತಿಯುತ ದೂರದರ್ಶಕಗಳು ಅಥವಾ ವೈದ್ಯಕೀಯ ಮತ್ತು ಜೀವಶಾಸ್ತ್ರದಲ್ಲಿ ಬಳಸುವ ಸೂಕ್ಷ್ಮದರ್ಶಕಗಳವರೆಗೆ ಎಲ್ಲವನ್ನೂ ಒಳಗೊಂಡಿದೆ.
- ಅಲ್ಟ್ರಾಸೌಂಡ್ ಸಾಧನಗಳು ಅದೇ ತತ್ವವನ್ನು ಸಹ ಬಳಸಿ. ಅಲ್ಟ್ರಾಸೌಂಡ್ ಉಪಕರಣಗಳು ನಿಖರವಾದ ಪರೀಕ್ಷೆಗಳನ್ನು ಅನುಮತಿಸುತ್ತದೆ. X- ಕಿರಣಗಳು ಅದೇ ತತ್ವಗಳ ಪ್ರಕಾರ ಹರಡುತ್ತವೆ.
- ಮೈಕ್ರೋವೇವ್ ಓವನ್ಗಳು - ಆಚರಣೆಯಲ್ಲಿ ಪ್ರಶ್ನೆಯಲ್ಲಿರುವ ಕಾನೂನಿನ ಅನ್ವಯದ ಮತ್ತೊಂದು ಉದಾಹರಣೆ. ಅತಿಗೆಂಪು ವಿಕಿರಣದ ಕಾರಣದಿಂದಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುವ ಎಲ್ಲಾ ಸಾಧನಗಳನ್ನು ಸಹ ಇದು ಒಳಗೊಂಡಿದೆ (ಉದಾಹರಣೆಗೆ, ರಾತ್ರಿ ದೃಷ್ಟಿ ಸಾಧನಗಳು).
- ಕಾನ್ಕೇವ್ ಕನ್ನಡಿಗಳು ಕಾರ್ಯಕ್ಷಮತೆಯನ್ನು ಹೆಚ್ಚಿಸಲು ಬ್ಯಾಟರಿ ದೀಪಗಳು ಮತ್ತು ದೀಪಗಳನ್ನು ಅನುಮತಿಸಿ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಬೆಳಕಿನ ಬಲ್ಬ್ನ ಶಕ್ತಿಯು ಕನ್ನಡಿ ಅಂಶದ ಬಳಕೆಯಿಲ್ಲದೆ ಕಡಿಮೆ ಇರುತ್ತದೆ.
ಅಂದಹಾಗೆ! ಬೆಳಕಿನ ಪ್ರತಿಫಲನದ ಮೂಲಕ, ನಾವು ಚಂದ್ರ ಮತ್ತು ನಕ್ಷತ್ರಗಳನ್ನು ನೋಡುತ್ತೇವೆ.
ಬೆಳಕಿನ ಪ್ರತಿಬಿಂಬದ ನಿಯಮವು ಅನೇಕ ನೈಸರ್ಗಿಕ ವಿದ್ಯಮಾನಗಳನ್ನು ವಿವರಿಸುತ್ತದೆ ಮತ್ತು ಅದರ ವೈಶಿಷ್ಟ್ಯಗಳ ಜ್ಞಾನವು ನಮ್ಮ ಕಾಲದಲ್ಲಿ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುವ ಸಾಧನಗಳನ್ನು ರಚಿಸಲು ಸಾಧ್ಯವಾಗಿಸಿತು.